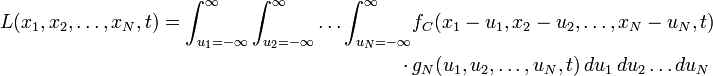Scale Space Implementation

Scale Space Implementation

The linear scale-space representation of an N-dimensional continuous signal is obtained by convolving with an N-dimensional Gaussian kernel

\begin{align} L(x_1, x_2, \dots, x_N, t) = \int_{u_1=-\infty}^{\infty} \int_{u_2=-\infty}^{\infty} \dots \int_{u_N=-\infty}^{\infty} &f_C(x_1-u_1, x_2-u_2, \dots, x_N-u_N, t)\\ \, \cdot \, &g_N(u_1, u_2, \dots, u_N, t) \, du_1 \, du_2 \dots du_N \end{align}

However, for implementation, this definition is impractical, since it is continuous. When applying the scale space concept to a discrete signal, different approaches can be taken. This article is a brief summary of some of the most frequently used methods.

Read more about Scale Space Implementation:  Separability, The Sampled Gaussian Kernel, The Discrete Gaussian Kernel, Recursive Filters, Finite-impulse-response (FIR) Smoothers, Real-time Implementation Within Pyramids and Discrete Approximation of Scale-normalized Derivatives, Other Multi-scale Approaches, See Also

Famous quotes containing the words scale and/or space:

    “Every man needs slaves like he needs clean air. To rule is to breathe, is it not? And even the most disenfranchised get to breathe. The lowest on the social scale have their spouses or their children.”
    —Albert Camus (1913–1960)

    “Though seas and land be ‘twixt us both,
    Our faith and troth,
    Like separated souls,
    All time and space controls:
    Above the highest sphere we meet
    Unseen, unknown, and greet as angels greet.”
    —Richard Lovelace (1618–1658)