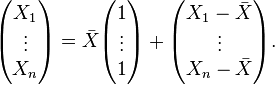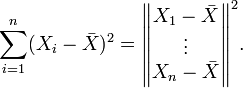Degrees of Freedom of A Random Vector
Geometrically, the degrees of freedom can be interpreted as the dimension of certain vector subspaces. As a starting point, suppose that we have a sample of n independent normally distributed observations,
- .
This can be represented as an n-dimensional random vector:
Since this random vector can lie anywhere in n-dimensional space, it has n degrees of freedom.
Now, let be the sample mean. The random vector can be decomposed as the sum of the sample mean plus a vector of residuals:
The first vector on the right-hand side is constrained to be a multiple of the vector of 1's, and the only free quantity is . It therefore has 1 degree of freedom.
The second vector is constrained by the relation . The first n − 1 components of this vector can be anything. However, once you know the first n − 1 components, the constraint tells you the value of the nth component. Therefore, this vector has n − 1 degrees of freedom.
Mathematically, the first vector is the orthogonal, or least-squares, projection of the data vector onto the subspace spanned by the vector of 1's. The 1 degree of freedom is the dimension of this subspace. The second residual vector is the least-squares projection onto the (n − 1)-dimensional orthogonal complement of this subspace, and has n − 1 degrees of freedom.
In statistical testing applications, often one isn't directly interested in the component vectors, but rather in their squared lengths. In the example above, the residual sum-of-squares is
If the data points are normally distributed with mean 0 and variance, then the residual sum of squares has a scaled chi-squared distribution (scaled by the factor ), with n − 1 degrees of freedom. The degrees-of-freedom, here a parameter of the distribution, can still be interpreted as the dimension of an underlying vector subspace.
Likewise, the one-sample t-test statistic,
follows a Student's t distribution with n − 1 degrees of freedom when the hypothesized mean is correct. Again, the degrees-of-freedom arises from the residual vector in the denominator.
Read more about this topic: Degrees Of Freedom (statistics)
Famous quotes containing the words degrees of, degrees, freedom and/or random:
“So that the life of a writer, whatever he might fancy to the contrary, was not so much a state of composition, as a state of warfare; and his probation in it, precisely that of any other man militant upon earth,—both depending alike, not half so much upon the degrees of his WIT—as his RESISTANCE.”
—Laurence Sterne (1713–1768)
“So that the life of a writer, whatever he might fancy to the contrary, was not so much a state of composition, as a state of warfare; and his probation in it, precisely that of any other man militant upon earth,—both depending alike, not half so much upon the degrees of his WIT—as his RESISTANCE.”
—Laurence Sterne (1713–1768)
“Today we seek a moral basis for peace.... It cannot be a lasting peace if the fruit of it is oppression, or starvation, cruelty, or human life dominated by armed camps. It cannot be a sound peace if small nations must live in fear of powerful neighbors. It cannot be a moral peace if freedom from invasion is sold for tribute.”
—Franklin D. Roosevelt (1882–1945)
“There is a potential 4-6 percentage point net gain for the President [George Bush] by replacing Dan Quayle on the ticket with someone of neutral stature.”
—Mary Matalin, U.S. Republican political advisor, author, and James Carville b. 1946, U.S. Democratic political advisor, author. All’s Fair: Love, War, and Running for President, p. 205, Random House (1994)