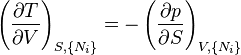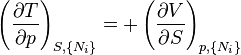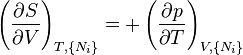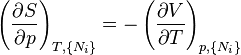Thermodynamic Potential - The Maxwell Relations

The Maxwell Relations

Again, define and to be conjugate pairs, and the to be the natural variables of some potential . We may take the "cross differentials" of the state equations, which obey the following relationship:

\left(\frac{\partial}{\partial y_j} \left(\frac{\partial \Phi}{\partial y_k} \right)_{\{y_{i\ne k}\}} \right)_{\{y_{i\ne j}\}} = \left(\frac{\partial}{\partial y_k} \left(\frac{\partial \Phi}{\partial y_j} \right)_{\{y_{i\ne j}\}} \right)_{\{y_{i\ne k}\}}

From these we get the Maxwell relations. There will be (D-1)/2 of them for each potential giving a total of D(D-1)/2 equations in all. If we restrict ourselves the U, F, H, G

\left(\frac{\partial T}{\partial V}\right)_{S,\{N_i\}} = -\left(\frac{\partial p}{\partial S}\right)_{V,\{N_i\}}
\left(\frac{\partial T}{\partial p}\right)_{S,\{N_i\}} = +\left(\frac{\partial V}{\partial S}\right)_{p,\{N_i\}}
\left(\frac{\partial S}{\partial V}\right)_{T,\{N_i\}} = +\left(\frac{\partial p}{\partial T}\right)_{V,\{N_i\}}
\left(\frac{\partial S}{\partial p}\right)_{T,\{N_i\}} = -\left(\frac{\partial V}{\partial T}\right)_{p,\{N_i\}}

Using the equations of state involving the chemical potential we get equations such as:

\left(\frac{\partial T}{\partial N_j}\right)_{V,S,\{N_{i\ne j}\}} = \left(\frac{\partial \mu_j}{\partial S}\right)_{V,\{N_i\}}

and using the other potentials we can get equations such as:

\left(\frac{\partial N_j}{\partial V}\right)_{S,\mu_j,\{N_{i\ne j}\}} = -\left(\frac{\partial p}{\partial \mu_j}\right)_{S,V\{N_{i\ne j}\}}
\left(\frac{\partial N_j}{\partial N_k}\right)_{S,V,\mu_j,\{N_{i\ne j,k}\}} = -\left(\frac{\partial \mu_k}{\partial \mu_j}\right)_{S,V\{N_{i\ne j}\}}

Read more about this topic:  Thermodynamic Potential

Famous quotes containing the words maxwell and/or relations:

    “Gin a body meet a body
    Flyin’ through the air,
    Gin a body hit a body,
    Will it fly? and where?”
    —James Clerk Maxwell (1831–1879)

    “Happy will that house be in which the relations are formed from character; after the highest, and not after the lowest order; the house in which character marries, and not confusion and a miscellany of unavowable motives.”
    —Ralph Waldo Emerson (1803–1882)