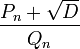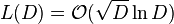Length of The Repeating Block
By analyzing the sequence of combinations
that can possibly arise when ζ = (P + √D)/Q is expanded as a regular continued fraction, Lagrange showed that the largest partial denominator ai in the expansion is less than 2√D, and that the length of the repeating block is less than 2D.
More recently, sharper arguments based on the divisor function have shown that L(D), the length of the repeating block for a quadratic surd of discriminant D, is given by
where the big O means "on the order of", or "asymptotically proportional to" (see big O notation).
Read more about this topic: Periodic Continued Fraction
Famous quotes containing the words length of, length, repeating and/or block:
“An ... important antidote to American democracy is American gerontocracy. The positions of eminence and authority in Congress are allotted in accordance with length of service, regardless of quality. Superficial observers have long criticized the United States for making a fetish of youth. This is unfair. Uniquely among modern organs of public and private administration, its national legislature rewards senility.”
—John Kenneth Galbraith (b. 1908)
“With the ancient is wisdom; and in length of days understanding.”
—Bible: Hebrew Job, 12:12.
“We can best help you to prevent war not by repeating your words and following your methods but by finding new words and creating new methods.”
—Virginia Woolf (1882–1941)
“For Jews demand signs and Greeks desire wisdom, but we proclaim Christ crucified, a stumbling block to Jews and foolishness to Gentiles...”
—Bible: New Testament, 1 Corinthians 1:22-3.