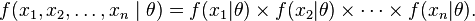Maximum Likelihood - Principles

Principles

Suppose there is a sample x1, x2, ..., xn of n independent and identically distributed observations, coming from a distribution with an unknown probability density function f0(·). It is however surmised that the function f0 belongs to a certain family of distributions { f(·| θ), θ ∈ Θ }, called the parametric model, so that f0 = f(·| θ0). The value θ0 is unknown and is referred to as the true value of the parameter. It is desirable to find an estimator which would be as close to the true value θ0 as possible. Both the observed variables xi and the parameter θ can be vectors.

To use the method of maximum likelihood, one first specifies the joint density function for all observations. For an independent and identically distributed sample, this joint density function is

f(x_1,x_2,\ldots,x_n\;|\;\theta) = f(x_1|\theta)\times f(x_2|\theta) \times \cdots \times f(x_n|\theta).

Now we look at this function from a different perspective by considering the observed values x1, x2, ..., xn to be fixed "parameters" of this function, whereas θ will be the function's variable and allowed to vary freely; this function will be called the likelihood:

\mathcal{L}(\theta\,|\,x_1,\ldots,x_n) = f(x_1,x_2,\ldots,x_n\;|\;\theta) = \prod_{i=1}^n f(x_i|\theta).

In practice it is often more convenient to work with the logarithm of the likelihood function, called the log-likelihood:

\ln\mathcal{L}(\theta\,|\,x_1,\ldots,x_n) = \sum_{i=1}^n \ln f(x_i|\theta),

or the average log-likelihood:

\hat\ell = \frac1n \ln\mathcal{L}.

The hat over ℓ indicates that it is akin to some estimator. Indeed, estimates the expected log-likelihood of a single observation in the model.

The method of maximum likelihood estimates θ0 by finding a value of θ that maximizes . This method of estimation defines a maximum-likelihood estimator (MLE) of θ0

\{ \hat\theta_\mathrm{mle}\} \subseteq \{ \underset{\theta\in\Theta}{\operatorname{arg\,max}}\ \hat\ell(\theta\,|\,x_1,\ldots,x_n) \}.

if any maximum exists. An MLE estimate is the same regardless of whether we maximize the likelihood or the log-likelihood function, since log is a monotonically increasing function.

For many models, a maximum likelihood estimator can be found as an explicit function of the observed data x1, ..., xn. For many other models, however, no closed-form solution to the maximization problem is known or available, and an MLE has to be found numerically using optimization methods. For some problems, there may be multiple estimates that maximize the likelihood. For other problems, no maximum likelihood estimate exists (meaning that the log-likelihood function increases without attaining the supremum value).

In the exposition above, it is assumed that the data are independent and identically distributed. The method can be applied however to a broader setting, as long as it is possible to write the joint density function f(x1, ..., xn | θ), and its parameter θ has a finite dimension which does not depend on the sample size n. In a simpler extension, an allowance can be made for data heterogeneity, so that the joint density is equal to f1(x1|θ) · f2(x2|θ) · ··· · fn(xn | θ). In the more complicated case of time series models, the independence assumption may have to be dropped as well.

A maximum likelihood estimator coincides with the most probable Bayesian estimator given a uniform prior distribution on the parameters.

Read more about this topic:  Maximum Likelihood

Famous quotes containing the word principles:

    “It must appear impossible, that theism could, from reasoning, have been the primary religion of human race, and have afterwards, by its corruption, given birth to polytheism and to all the various superstitions of the heathen world. Reason, when obvious, prevents these corruptions: When abstruse, it keeps the principles entirely from the knowledge of the vulgar, who are alone liable to corrupt any principle or opinion.
    ”
    —David Hume (1711–1776)

    “I cannot consent that my mortal body shall be laid in a repository prepared for an Emperor or a King—my republican feelings and principles forbid it—the simplicity of our system of government forbids it.”
    —Andrew Jackson (1767–1845)

    “The chief lesson of the Depression should never be forgotten. Even our liberty-loving American people will sacrifice their freedom and their democratic principles if their security and their very lives are threatened by another breakdown of our free enterprise system. We can no more afford another general depression than we can afford another total war, if democracy is to survive.”
    —Agnes E. Meyer (1887–1970)