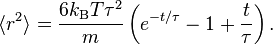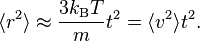Equipartition Theorem - Applications - Brownian Motion

Brownian Motion

See also: Brownian motion

The equipartition theorem can be used to derive the Brownian motion of a particle from the Langevin equation. According to that equation, the motion of a particle of mass m with velocity v is governed by Newton's second law

\frac{d\mathbf{v}}{dt} = \frac{1}{m} \mathbf{F} = -\frac{\mathbf{v}}{\tau} + \frac{1}{m} \mathbf{F}_{\mathrm{rnd}},

where Frnd is a random force representing the random collisions of the particle and the surrounding molecules, and where the time constant τ reflects the drag force that opposes the particle's motion through the solution. The drag force is often written Fdrag = −γv; therefore, the time constant τ equals m/γ.

The dot product of this equation with the position vector r, after averaging, yields the equation

\Bigl\langle \mathbf{r} \cdot \frac{d\mathbf{v}}{dt} \Bigr\rangle + \frac{1}{\tau} \langle \mathbf{r} \cdot \mathbf{v} \rangle = 0

for Brownian motion (since the random force Frnd is uncorrelated with the position r). Using the mathematical identities

\frac{d}{dt} \left( \mathbf{r} \cdot \mathbf{r} \right) = \frac{d}{dt} \left( r^{2} \right) = 2 \left( \mathbf{r} \cdot \mathbf{v} \right)

and

\frac{d}{dt} \left( \mathbf{r} \cdot \mathbf{v} \right) = v^{2} + \mathbf{r} \cdot \frac{d\mathbf{v}}{dt},

the basic equation for Brownian motion can be transformed into

\frac{d^{2}}{dt^{2}} \langle r^{2} \rangle + \frac{1}{\tau} \frac{d}{dt} \langle r^{2} \rangle = 2 \langle v^{2} \rangle = \frac{6}{m} k_{\rm B} T,

where the last equality follows from the equipartition theorem for translational kinetic energy:

\langle H_{\mathrm{kin}} \rangle = \Bigl\langle \frac{p^{2}}{2m} \Bigr\rangle = \langle \tfrac{1}{2} m v^{2} \rangle = \tfrac{3}{2} k_{\rm B} T.

The above differential equation for (with suitable initial conditions) may be solved exactly:

\langle r^{2} \rangle = \frac{6k_{\rm B} T \tau^{2}}{m} \left( e^{-t/\tau} - 1 + \frac{t}{\tau} \right).

On small time scales, with t << τ, the particle acts as a freely moving particle: by the Taylor series of the exponential function, the squared distance grows approximately quadratically:

\langle r^{2} \rangle \approx \frac{3k_{\rm B} T}{m} t^{2} = \langle v^{2} \rangle t^{2}.

However, on long time scales, with t >> τ, the exponential and constant terms are negligible, and the squared distance grows only linearly:

\langle r^{2} \rangle \approx \frac{6k_{B} T\tau}{m} t = \frac{6 k_{B} T t}{\gamma}.

This describes the diffusion of the particle over time. An analogous equation for the rotational diffusion of a rigid molecule can be derived in a similar way.

Read more about this topic:  Equipartition Theorem, Applications

Famous quotes containing the word motion:

    “Motion or change, and identity or rest, are the first and second secrets of nature: Motion and Rest. The whole code of her laws may be written on the thumbnail, or the signet of a ring.”
    —Ralph Waldo Emerson (1803–1882)