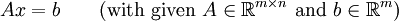In linear algebra, a constrained generalized inverse inverse is obtained by solving a system of linear equations with an additional constraint that the solution is in a given subspace. One also says that the problem is described by a system of constrained linear equations.
In many practical problems, the solution of a linear system of equations
is acceptable only when it is in a certain linear subspace of .
In the following, the orthogonal projection on will be denoted by . Constrained system of linear equations
has a solution if and only if the unconstrained system of equations
is solvable. If the subspace is a proper subspace of, then the matrix of the unconstrained problem may be singular even if the system matrix of the constrained problem is invertible (in that case, ). This means that one needs to use a generalized inverse for the solution of the constrained problem. So, a generalized inverse of is also called a -constrained pseudoinverse of .
An example of a pseudoinverse that can be used for the solution of a constrained problem is the Bott-Duffin inverse of constrained to, which is defined by the equation
if the inverse on the right-hand-side exists.
Famous quotes containing the words constrained, generalized and/or inverse:
“An expansive life, one not constrained by four walls, requires as well an expansive pocket.”
—Anton Pavlovich Chekhov (1860–1904)
“One is conscious of no brave and noble earnestness in it, of no generalized passion for intellectual and spiritual adventure, of no organized determination to think things out. What is there is a highly self-conscious and insipid correctness, a bloodless respectability submergence of matter in manner—in brief, what is there is the feeble, uninspiring quality of German painting and English music.”
—H.L. (Henry Lewis)
“Yet time and space are but inverse measures of the force of the soul. The spirit sports with time.”
—Ralph Waldo Emerson (1803–1882)