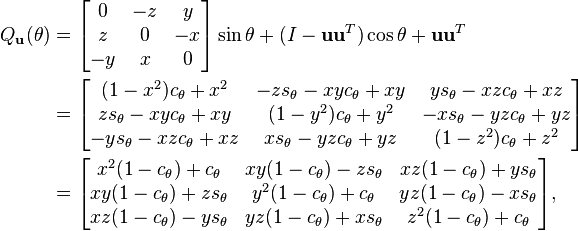Rotation Matrix - Decompositions - Nested Dimensions

Nested Dimensions

A 3×3 rotation matrix like

suggests a 2×2 rotation matrix,

is embedded in the upper left corner:

This is no illusion; not just one, but many, copies of n-dimensional rotations are found within (n+1)-dimensional rotations, as subgroups. Each embedding leaves one direction fixed, which in the case of 3×3 matrices is the rotation axis. For example, we have

fixing the x axis, the y axis, and the z axis, respectively. The rotation axis need not be a coordinate axis; if u = (x,y,z) is a unit vector in the desired direction, then

where c_θ = cos θ, s_θ = sin θ, is a rotation by angle θ leaving axis u fixed.

A direction in (n+1)-dimensional space will be a unit magnitude vector, which we may consider a point on a generalized sphere, Sn. Thus it is natural to describe the rotation group SO(n+1) as combining SO(n) and Sn. A suitable formalism is the fiber bundle,

where for every direction in the "base space", Sn, the "fiber" over it in the "total space", SO(n+1), is a copy of the "fiber space", SO(n), namely the rotations that keep that direction fixed.

Thus we can build an n×n rotation matrix by starting with a 2×2 matrix, aiming its fixed axis on S2 (the ordinary sphere in three-dimensional space), aiming the resulting rotation on S3, and so on up through Sn−1. A point on Sn can be selected using n numbers, so we again have n(n−1)/2 numbers to describe any n×n rotation matrix.

In fact, we can view the sequential angle decomposition, discussed previously, as reversing this process. The composition of n−1 Givens rotations brings the first column (and row) to (1,0,…,0), so that the remainder of the matrix is a rotation matrix of dimension one less, embedded so as to leave (1,0,…,0) fixed.