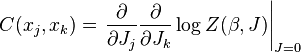Partition Function (mathematics) - Correlation Functions

Correlation Functions

By introducing artificial auxiliary functions into the partition function, it can then be used to obtain the expectation value of the random variables. Thus, for example, by writing

\begin{align} Z(\beta,J) & = Z(\beta,J_1,J_2,\dots) \\ & = \sum_{x_i} \exp \left(-\beta H(x_1,x_2,\dots) + \sum_n J_n x_n \right) \end{align}

one then has

\bold{E} = \langle x_k \rangle = \left. \frac{\partial}{\partial J_k} \log Z(\beta,J)\right|_{J=0}

as the expectation value of . In the path integral formulation of quantum field theory, these auxiliary functions are commonly referred to as source fields.

Multiple differentiations lead to the correlation functions of the random variables. Thus the correlation function between variables and is given by:

C(x_j,x_k) = \left. \frac{\partial}{\partial J_j} \frac{\partial}{\partial J_k} \log Z(\beta,J)\right|_{J=0}

For the case where H can be written as a quadratic form involving a differential operator, that is, as

then the correlation function can be understood to be the Green's function for the differential operator (and generally giving rise to Fredholm theory). In the quantum field theory setting, such functions are referred to as propagators; higher order correlators are called n-point functions; working with them defines the effective action of a theory.

Read more about this topic:  Partition Function (mathematics)

Famous quotes containing the word functions:

    “Mark the babe
    Not long accustomed to this breathing world;
    One that hath barely learned to shape a smile,
    Though yet irrational of soul, to grasp
    With tiny finger—to let fall a tear;
    And, as the heavy cloud of sleep dissolves,
    To stretch his limbs, bemocking, as might seem,
    The outward functions of intelligent man.”
    —William Wordsworth (1770–1850)