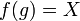Formal Power Series - Interpreting Formal Power Series As Functions

Interpreting Formal Power Series As Functions

In mathematical analysis, every convergent power series defines a function with values in the real or complex numbers. Formal power series can also be interpreted as functions, but one has to be careful with the domain and codomain. If f = ∑an Xn is an element of R], S is a commutative associative algebra over R, I is an ideal in S such that the I-adic topology on S is complete, and x is an element of I, then we can define

f(X) = \sum_{n\ge 0} a_n X^n.

This latter series is guaranteed to converge in S given the above assumptions on X. Furthermore, we have

and

Unlike in the case of bona fide functions, these formulas are not definitions but have to be proved.

Since the topology on R] is the (X)-adic topology and R] is complete, we can in particular apply power series to other power series, provided that the arguments don't have constant coefficients (so that they belong to the ideal (X)): f(0), f(X2−X) and f( (1 − X)−1 − 1) are all well defined for any formal power series f∈R].

With this formalism, we can give an explicit formula for the multiplicative inverse of a power series f whose constant coefficient a = f(0) is invertible in R:

f^{-1} = \sum_{n \ge 0} a^{-n-1} (a-f)^n.

If the formal power series g with g(0) = 0 is given implicitly by the equation

f(g) = X \,

where f is a known power series with f(0) = 0, then the coefficients of g can be explicitly computed using the Lagrange inversion formula.

Read more about this topic:  Formal Power Series

Famous quotes containing the words interpreting, formal, power, series and/or functions:

    “Drawing is a struggle between nature and the artist, in which the better the artist understands the intentions of nature, the more easily he will triumph over it. For him it is not a question of copying, but of interpreting in a simpler and more luminous language.”
    —Charles Baudelaire (1821–1867)

    “True variety is in that plenitude of real and unexpected elements, in the branch charged with blue flowers thrusting itself, against all expectations, from the springtime hedge which seems already too full, while the purely formal imitation of variety ... is but void and uniformity, that is, that which is most opposed to variety....”
    —Marcel Proust (1871–1922)

    “Relying ... on the patronage of your good will, I advance with obedience to the work, ready to retire from it whenever you become sensible how much better choice it is in your power to make.”
    —Thomas Jefferson (1743–1826)

    “If the technology cannot shoulder the entire burden of strategic change, it nevertheless can set into motion a series of dynamics that present an important challenge to imperative control and the industrial division of labor. The more blurred the distinction between what workers know and what managers know, the more fragile and pointless any traditional relationships of domination and subordination between them will become.”
    —Shoshana Zuboff (b. 1951)

    “Adolescents, for all their self-involvement, are emerging from the self-centeredness of childhood. Their perception of other people has more depth. They are better equipped at appreciating others’ reasons for action, or the basis of others’ emotions. But this maturity functions in a piecemeal fashion. They show more understanding of their friends, but not of their teachers.”
    —Terri Apter (20th century)