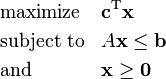Linear programming (LP, or linear optimization) is a mathematical method for determining a way to achieve the best outcome (such as maximum profit or lowest cost) in a given mathematical model for some list of requirements represented as linear relationships. Linear programming is a specific case of mathematical programming (mathematical optimization).
More formally, linear programming is a technique for the optimization of a linear objective function, subject to linear equality and linear inequality constraints. Its feasible region is a convex polyhedron, which is a set defined as the intersection of finitely many half spaces, each of which is defined by a linear inequality. Its objective function is a real-valued affine function defined on this polyhedron. A linear programming algorithm finds a point in the polyhedron where this function has the smallest (or largest) value if such a point exists.
Linear programs are problems that can be expressed in canonical form:
where x represents the vector of variables (to be determined), c and b are vectors of (known) coefficients, A is a (known) matrix of coefficients, and is the matrix transpose. The expression to be maximized or minimized is called the objective function (cTx in this case). The inequalities Ax ≤ b are the constraints which specify a convex polytope over which the objective function is to be optimized. In this context, two vectors are comparable when they have the same dimensions. If every entry in the first is less-than or equal-to the corresponding entry in the second then we can say the first vector is less-than or equal-to the second vector.
Linear programming can be applied to various fields of study. It is used in business and economics, but can also be utilized for some engineering problems. Industries that use linear programming models include transportation, energy, telecommunications, and manufacturing. It has proved useful in modeling diverse types of problems in planning, routing, scheduling, assignment, and design.
Read more about Linear Programming: History, Uses, Standard Form, Augmented Form (slack Form), Duality, Covering-packing Dualities, Complementary Slackness, Open Problems and Recent Work, Integer Unknowns, Integral Linear Programs, Solvers and Scripting (programming) Languages
Famous quotes containing the word programming:
“If there is a price to pay for the privilege of spending the early years of child rearing in the driver’s seat, it is our reluctance, our inability, to tolerate being demoted to the backseat. Spurred by our success in programming our children during the preschool years, we may find it difficult to forgo in later states the level of control that once afforded us so much satisfaction.”
—Melinda M. Marshall (20th century)